Structure And Properties Of Dental Materials Notes

Structure And Properties Of Dental Materials

All materials are made up of atoms. If the reaction of a material and its properties are to be predicted, a basic knowledge of matter is essential. All dental restorations, whether they be ceramic, plastic or metal, are built from atoms.

Structure of Matter

• Atom An atom is the smallest unit of matter that defines the chemical elements. Atoms are very small. The size of atoms is measured in picometers, which is trillionths (10–12) of a meter. Every atom is composed of a nucleus and one or more electrons that orbit the nucleus.

Read And Learn More: Basic Dental Materials Notes

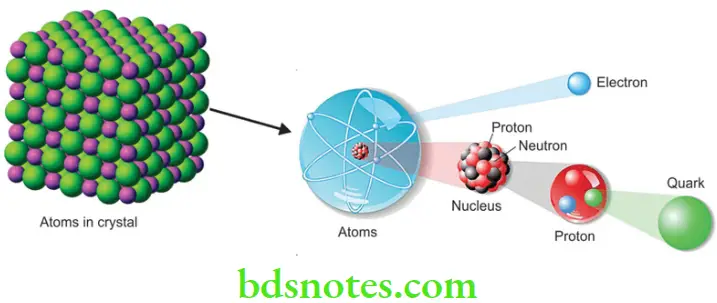
• Protons, neutrons, and electrons The nucleus is made of one or more protons and neutrons. Over 99.94% of the atom’s mass is in the nucleus. The protons have a positive electric charge, the electrons have a negative electric charge, and the neutrons have no electric charge. If the number of protons and electrons is equal, that atom is electrically neutral. If an atom has in excess or lesser number of electrons relative to protons, then it has an overall positive or negative charge and is called an ion.
  • Electrons of an atom are attracted to the protons in an atomic nucleus by the electromagnetic force. The protons and neutrons in the nucleus are attracted to each other by a different force, the nuclear force, which is usually stronger than the electromagnetic force repelling the positively charged protons from one another. The number of protons in the nucleus defines to what chemical element the atom belongs, for example, all copper atoms contain 29 protons.
• Quarks Protons and neutrons are made up of subatomic particles called quarks. Quarks are believed to be the basic building blocks of matter.

Interatomic Bonds

Atoms are held together by some force. These interatomic bonding forces that hold atoms together are cohesive forces.

Interatomic bonds may be classified as

• Primary bonds, or
• Secondary bonds

Primary Bonds

These are chemical in nature.

• Ionic
• Covalent
• Metallic

Ionic Bonds These are simple chemical bonds, resulting from mutual attraction of positive and negative charges. The classic example is sodium chloride Na+ Cl¯.

Covalent Bonds In many chemical compounds, two valence electrons are shared. The hydrogen molecule (H2) is an example of covalent bonding. Another example is methane. The carbon atom has 4 valence electrons that can be stabilized by joining with hydrogen.

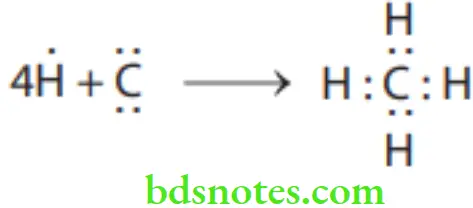
Metallic Bonds One of the chief characteristics of a metal is its ability to conduct heat and electricity. Such conduction is due to the mobility of the so-called free electrons present in the metals. The outer shield valence electrons can be removed easily from the metallic atom leaving the balance of the electrons tied to the nucleus, thus forming a positive ion. The free valence electrons can move about in the metal space lattice to form what is, sometimes, described as an electron ‘cloud’ or ‘gas’. The electrostatic attraction between this electron ‘cloud’ and the positive ions in the lattice bonds the metal atoms together as a solid.

Secondary Bonds (Van der Waals forces)

• A second type of bond between molecules may be seen. They are also known as van der Waals forces (named after Dutch scientist Johannes Diderik van der Waals. They differ from covalent and ionic bonding in that they are caused by correlations in the fluctuating polarizations (dipole) of nearby particles. They are defined as weak, short-range electrostatic attractive forces between uncharged molecules, arising from the interaction of permanent or transient electric dipole moments.
• Dipole van der Waals Forces are due to the formation of dipole. A dipole is formed when electrons shift to one side of the atoms or molecules resulting in the formation of a negative polarity on the side and the other half a positive polarity. This attracts other similar dipoles.
• There are three kinds of van der Waals forces – 1. Keesom force (between two permanent dipoles), 2. Debye force (between a permanent dipole and an induced dipole) 3. London dispersion force (between two instantaneously induced dipoles).
• Van der Waals forces are relatively weak compared to covalent bonds but play a fundamental role in fields as diverse as supramolecular chemistry, structural biology, polymer science, nanotechnology, surface science, and condensed matter physics. Van der Waals forces define many properties of organic compounds. In nature, geckos and spiders utilize van der Waals forces to climb and cling onto smooth surfaces.

Crystal Structure

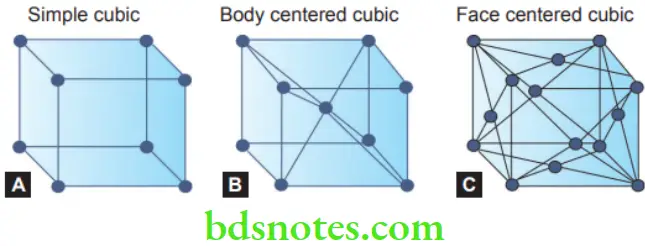
• A space lattice or crystal can be defined as any arrangement of atoms in space such that every atom is situated similarly to every atom. Space lattice may be the result of primary or secondary bonds.
• There are 14 possible lattice-type forms, but many of the metals used in dentistry belong to the cubic system. The simplest cubic space lattice. The solid circles represent the position of the atoms. Their positions are located at the points of intersection of three sets of parallel planes, each set being perpendicular to other planes. These planes are often referred to as crystal planes.

Noncrystalline Structure

• In a crystalline structure, the arrangement of atoms in the lattice is orderly and follows a particular pattern. In noncrystalline structures or amorphous structures, e.g. waxes, the arrangement of atoms in the lattice is disorderly and distributed at random.
• There is, however, a tendency for the arrangement of atoms or molecules to be regular, for example, glass is considered to be a noncrystalline solid, yet its atoms bind to form a short-range order rather than a long-range order lattice. In other words, the ordered arrangement of glass is localized with a large number of disordered units between the ordered units. Since such an arrangement is also typical of liquids, such solids are, sometimes, called supercooled liquids.

Stress And Strain

• The distance between two atoms is known as interatomic distance. This interatomic distance depends upon the electrostatic fields of the electrons. If the atoms come too close to each other, they are repelled from each other by their electron charges. On the other hand, forces of attraction keep them from separating. Thus the atoms are kept together at a position where these forces of repulsion and attraction become equal in magnitude (but opposite in direction). This is the normal equilibrium position of the atoms.
• The normal position of the atoms can be changed by the application of mechanical force. For example, the interatomic distance can be increased by a force pulling them apart. If the displacing force is measured across a given area it is known as a stress and the change in dimension is called a strain. In simple words, stress is the force applied and strain is the resulting change in shape.
• Theoretically, stress and strain exist whenever the interatomic distance is changed from the equilibrium position. If the stress pulling the atoms apart exceeds the resultant force of attraction, the atoms may separate, and the bonds holding them together are broken.
• Strain can also occur under compression. However, in this case, the strain produced is limited because when the atoms come closer than their normal interatomic distance, a sudden increase in energy is seen.

Diffusion

• The diffusion of molecules in gases and liquids is well known. However, molecules or atoms diffuse in the solid state as well. Diffusion rates depend mainly on the temperature. The higher the temperature, the greater will be the rate of diffusion. The diffusion rate will, however, vary with the atom size, and interatomic or intermolecular bonding lattice imperfections. Thus every material has its diffusion rate. The diffusion rate in noncrystalline materials may occur at a rapid rate and often may be seen.

Surface Tension

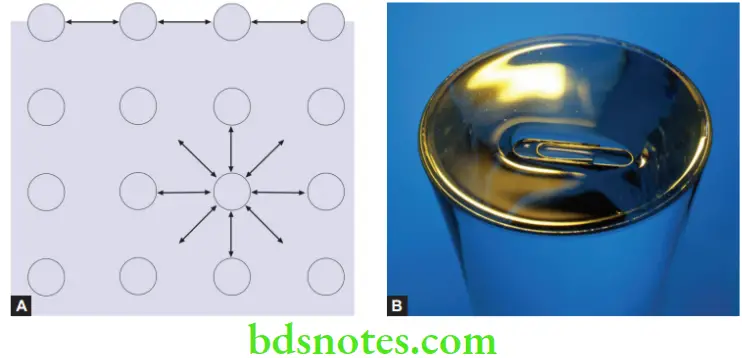
• The energy at the surface of a solid is greater than in its interior. For example, inside a lattice, all the atoms are equally attracted to each other. The interatomic distances are equal, and energy is minimal. However, at the surface of the lattice, the energy is greater because there are no atoms on the outside. Hence there is only a force from the inside of the lattice pulling the outermost atoms inwards. This creates tension on the outer surface and energy is needed to pull the outermost atoms away. The increase in energy per unit area of surface is referred to as surface energy or surface tension.
• The surface atoms of a solid tend to form bonds to any atom that comes close to the surface in order to reduce the surface energy of the solid. This attraction across the interface for unlike molecules is called adhesion. In summary, the greater the surface energy, the greater will be the adhesion capacity.

Wetting

• It is very difficult to force two solid surfaces to adhere. However smooth their surfaces may appear, they are likely to be very rough at the atomic or molecular level. When they are placed together, only the ‘hills’ or high spots are in contact. Since these areas form only a small percentage of the total surface, no adhesion takes place. For proper adhesion, the distance between the surface molecules should not be greater than 0.0007 micrometer or micron (µm).
• One method of overcoming this difficulty is to use a fluid that will flow into these irregularities and thus provide contact over a great part of the surface of the solid. For example, when two glass plates are placed one on top of the other, they do not usually adhere. However, if a film of water is placed in between them, it becomes difficult to separate the two plates.
• To produce adhesion in this manner, the liquid must flow easily over the entire surface and adhere to the solid. This characteristic is referred to as wetting. The degree of wetting is indicated by the contact angle of the adhesive to the adherend.

Contact angle

• The contact angle is the angle formed by the adhesive (e.g. water) and the adherend (e.g. glass) at their interface. The extent to which an adhesive will wet the surface of an adherend may be determined by measuring the contact angle between the adhesive and the adherend.
• Based on the contact angle there are four classes of wetting:
  • Contact Angle = 0 Perfect wetting
  • Contact Angle = 0 < <90° High wettability
  • Contact Angle = 90° ≤< 180° low wettability
  • Contact Angle = 180° Perfect non-wetting

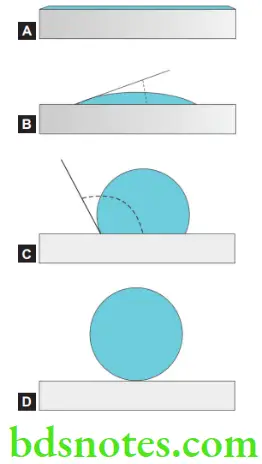
• If the forces of adhesion are stronger than the cohesive forces holding the molecules of the adhesive together, the liquid will spread completely over the surface of the solid and no angle will be formed (e.g. water on a soapy surface. If the liquid remains as a drop without spreading, the contact angle will be high.

Surfactant

• Surfactants are compounds that lower the surface tension (or interfacial tension) between two liquids or between a liquid and a solid. Surfactants may act as detergents, wetting agents, emulsifiers, foaming agents, and dispersants. Surfactants are added to some dental materials to improve wetting.

Significance

• The mouth is a highly moist environment and impression materials used in the mouth should be hydrophilic in order to record details even under moist conditions.
• Good wettability is again desired in the laboratory for products contacting gypsum products like dental stone and plaster which have a high moisture content. While pouring casts the stone should be able to get the impression well in order to minimize voids.
• Good wetting is important in soldering to produce a good strong joint.

Properties Of Dental Materials

To select and use a dental material one must understand its properties. Knowledge of the properties of the material predicts its behavior, functioning in the mouth, and longevity. Accordingly one can optimize design and techniques in order to get the best out of a particular material.

Various properties important to dental materials are

• Physical properties
• Mechanical properties
• Chemical properties
• Thermal properties
• Optical properties

Mechanical Dental Materials Properties

A mechanical property is the behavior of the material when it’s linked to the application of force. The mechanical properties of a material describe how it will react to physical forces.

Stress

• When a force acts on the body, tending to produce deformation, a resistance is developed within the body to this external force. The internal resistance of the body to the external force is called stress. Stress is equal and opposite in direction to the force (external) applied. This external force is also known as load.
• Since both applied force and internal resistance (stress) are distributed over a given area of the body, the stress in a structure is designated as a force per unit area.

Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{\mathrm{F}}{\mathrm{A}}\)

• The internal resistance to force (stress) is impractical to measure. The convenient way is to measure the external force applied to the cross-sectional area.
• The area over which the force acts is an important factor, especially in dental restorations in which areas over which the forces applied often are extremely small. Stress at a constant force is inversely proportional to the area—the smaller the area, the larger the stress, and vice versa.

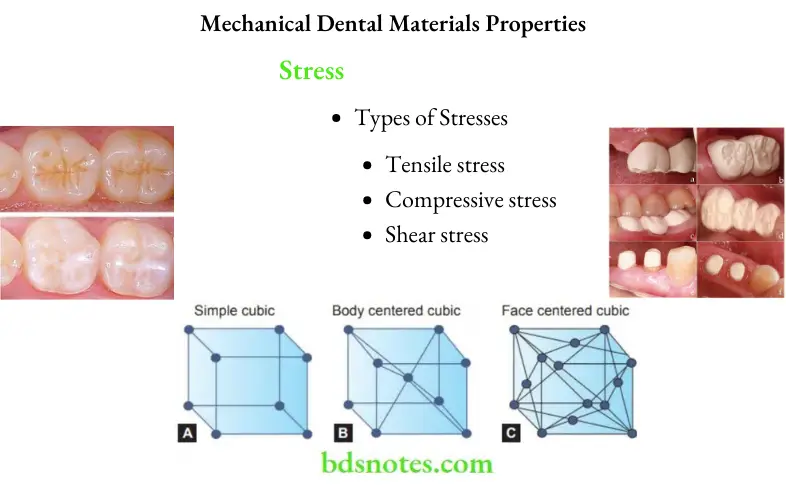
Types of Stresses

• Tensile stress
• Compressive stress
• Shear stress

Tensile stress

• Results in a body when it is subjected to two sets of forces that are directed away from each other in the same straight line. The load tends to stretch or elongate a body.

Compressive stress

• Results when the body is subjected to two sets of forces in the same straight line but directed toward each other. The load tends to shorten a body.

Shear stress

• Shear stress is a result of two forces directed parallel to each other. A stress that tends to resist a twisting motion, or a sliding of one portion of a body over another is a shear or shearing stress.

Strain

• If the stress (internal resistance) produced is not sufficient to withstand the external force (load) the body undergoes a change in shape (deformation). Each type of stress is capable of producing a corresponding deformation in the body. The deformation resulting from a tension, or pulling force, produces an elongation of a body, whereas a compression, or pushing force, causes compression or shortening of the body.

Strain = \(\frac{\text { Deformation or change in length }}{\text { Original length }}=\frac{\mathrm{E}}{\mathrm{L}}\)

• Strain is expressed as a change in length per unit length of the body when stress is applied. It is a dimensionless quantity and may be elastic or plastic or a combination of the two.

Complex Stresses

• It is difficult to induce just a single type of stress in a body. Whenever force is applied over a body, complex or multiple stresses are produced. These may be a combination of tensile, shear or compressive stresses. These multiple stresses are called complex stresses. For example, when a wire is stretched, the predominant stress is tensile, but shearing and compressive stresses will also be present because the wire is getting thinner (compressed in cross-section) as it elongates.

Poisson’s Ratio

• If we take a cylinder and subject it to tensile stress or compressive stress, there is simultaneous axial and lateral strain. Within the elastic range, the ratio of the lateral to the axial strain is called Poisson’s ratio.

Proportional Limit

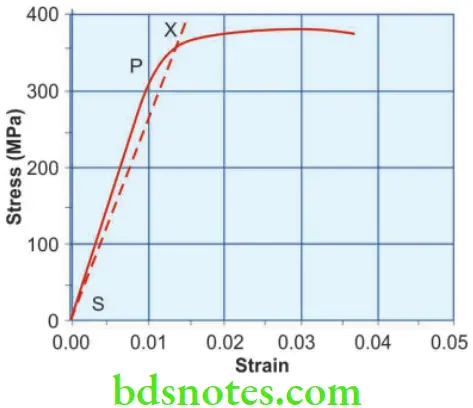
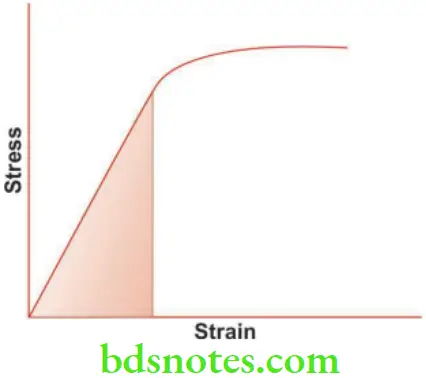
• A tensile load is applied to a wire in small increments until it breaks. If each stress is plotted on a vertical coordinate and the corresponding strain (change in length) is plotted on a horizontal coordinate, a curve is obtained. This is known as the stress-strain curve. It is useful to study some of the mechanical properties. The stress-strain curve is a straight line up to point ‘P’ after which it curves.
• The point ‘P’ is the proportional limit, i.e., up to point ‘P’ the stress is proportional to strain (Hooke’s Law). Beyond ‘P’ the strain is no longer elastic and so stress is no longer proportional to strain. Thus proportional stress can be defined as the greatest stress that may be produced in a material such that the stress is directly proportional to strain.

Elastic Limit

• Below the proportional limit (point ‘P’), a material is elastic in nature, that is, if the load is removed, the material will return to its original shape. Thus elastic limit may be defined as the maximum stress that a material will withstand without permanent deformation (change in shape).
• For all practical purposes, the elastic limit and the proportional limit represent the same stress. However the fundamental concept is different, one describes the elastic behavior of the material whereas the other deals with the proportionality of strain to stress in the structure.

Yield Strength

• Very few materials follow Hooke’s law perfectly and some permanent change may be seen in the tested material. A small amount of permanent strain is tolerable.
• The limit of tolerable permanent strain is the yield strength. Thus yield strength is defined as the stress at which a material exhibits a specified limiting deviation from proportionality of stress to strain.
• Determination of yield strength
  • How much permanent deformation can be tolerated? This varies from material to material and is determined by selecting an offset. An offset is an arbitrary value put for a material. It represents the percent of total permanent deformation that is acceptable for the material. In dentistry, 0.1% (1% offset) and 0.2% (2% offset) are most commonly used.
  • The yield strength is determined by selecting the desired offset and drawing a line parallel to the linear region of the stress-strain curve (Fig. 2.7). The point on the stress-strain curve where the offset meets is the yield strength (point X).

Modulus of Elasticity

• It is also referred to as ‘elastic modulus’ or ‘Young’s modulus’. It represents the relative stiffness or rigidity of the material within the elastic range.
• Young’s modulus is the ratio of stress to strain. Since stress is proportional to strain (up to the proportional limit), the stress-to-strain ratio would be constant.
  Modulus of elasticityorYoung’s modulus

⇒ \(E=\frac{\text { Stress }}{\text { Strain }}=\frac{\mathrm{F} / \mathrm{A}}{\mathrm{E} / \mathrm{L}}=\frac{\mathrm{FL}}{\mathrm{EA}}\)

• It, therefore, follows that the less the strain for a given stress, the greater the stiffness, e.g. if a wire is difficult to bend, considerable stress must be placed before a notable strain or deformation results. Such a material would possess a comparatively high modulus of elasticity.

Application

The metal frame of a metal-ceramic bridge should have a high stiffness. If the metal flexes, the porcelain veneer on it might crack or separate.

Flexibility

• Generally in dental practice, the material used as a restoration should withstand high stresses and show minimum deformation. However, there are instances where a large strain is needed with moderate or slight stress. For example, in an orthodontic appliance, a spring is often bent at a large distance with a small stress.
• In such a case the material is said to be flexible. The ‘Maximal flexibility’ is defined as the strain that occurs when the material is stressed to its proportional limit. The relation between the maximum flexibility, the proportional limit, and the modulus of elasticity may be expressed as

Maximum flexibility (EM)= \(\frac{\text { Proportional limit }(P)}{\text { Modulus of elasticity }(E)}\)

Application

• It is useful to know the flexibility of elastic impression materials to determine how easily they may be withdrawn over undercuts in the mouth.

Resilience

• Popularly, the term resilience is associated with ‘springiness’. Resilience can be defined as the amount of energy absorbed by a structure when it is stressed not to exceed its proportional 123 limits. For example, when an acrobat falls on a trapeze net the energy of his fall is absorbed by the resilience of the net, and when this energy is released, the acrobat is again thrown into the air.
• The resilience of a material is measured in terms of its modulus of resilience, which is the amount of energy stored in a body when a unit volume of a material is stressed to its proportional limit. It is expressed mathematically as

R (Modulus of Resilience) = \(\frac{\mathrm{P}^2 \text { (Proportional limit) }}{2 \mathrm{E} \text { (Modulus of elasticity) }}\)

• Resilience is also measured by the area under the straight line portion of the stress-strain curve.

Impact

It is the reaction of a stationary object to a collision with a moving object. Depending upon the resilience of the object, energy is stored in the body without causing deformation or with deformation.

The ability of a body to resist impact without permanent deformation is represented by the formula—KVR

where, K = Constant of proportionality

V = Volume

R = Modulus of resilience

But we know R = P2/2E

Therefore, impact resistance = \(\frac{\mathrm{KVP}^2}{2 \mathrm{E}}\)

From the above formula, we can conclude

Impact resistance will be decreased with an increase in the modulus of elasticity, which means that stiffer materials will have less impact resistance. Resilient materials will have better impact resistance (however, a high stiffness is also necessary to provide rigidity to a material under static loads, e.g. a cement base should be able to support an amalgam restoration). An increase in volume leads to an increase in impact resistance.

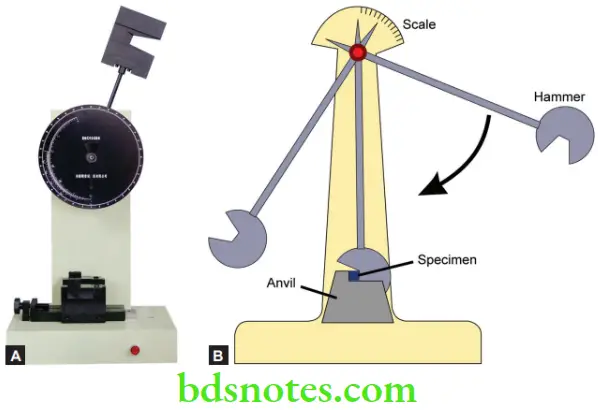
Impact Strength

• It is the energy required to fracture a material under an impact force. A Charpy-type impact tester is used. It has a heavy pendulum that swings down to fracture the specimen. Another instrument called the Izod impact tester can also be used.

Application

• Dentures should have a high impact strength to prevent it from breaking if accidentally dropped by the patient.

Permanent Deformation

• Once the elastic limit of a material is crossed by a specific amount of stress, the further increase in strain is called permanent deformation, i.e., the resulting change in dimension is permanent.

Application

• An elastic impression material deforms as it is removed from the mouth. However, due to its elastic nature, it recovers its shape and little permanent deformation occurs. Some materials are more elastic than others. Thus permanent deformation is higher in hydrocolloids than in elastomers.

Strength

The strength of a material is its resistance to fracture. It is measured by measuring the maximal stress required to fracture a structure.

The three types of strength are

• Tensile strength
• Compressive strength
• Shear strength

Tensile Strength

• Tensile strength is determined by subjecting a rod, wire, or dumbbell-shaped specimen to a tensile loading (a unilateral tension test). Tensile strength is defined as the maximal stress the structure will withstand before rupture.

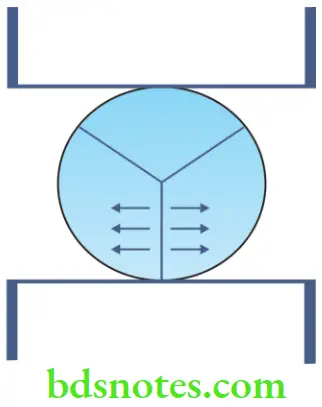
Tensile strength of brittle materials

• Brittle materials are difficult to test using the unilateral tension test. Instead, an indirect tensile test called the ‘diametral compression test’ (or Brazilian test) is used. In this method, a compressive load is placed on the diameter of a short cylindrical specimen. The tensile stress is directly proportional to the load applied as shown in the formula.

\(\text { Tensile-stress }=\frac{2 \mathrm{P}}{\pi \times \mathrm{D} \times \mathrm{T}}=\frac{\text { (load) }}{\pi \text { (diameter } \times \text { thickness })}\)

Compressive Strength

• Compressive strength or ‘crushing strength’ is determined by subjecting a cylindrical specimen to a compressive load. The strength value is obtained from the cross-sectional area and force applied. Though the load is compressive in nature, the failure is due to complex stresses.

Shear Strength

• Shear strength is the maximum stress that a material can withstand before failure in a shear mode of loading. It is tested using the punch or pushout method. The formula is as follows.

\(\text { Shear Strength }=\frac{\mathrm{F}}{\pi \mathrm{DH}}\)

Where F is the force

D is the punch diameter

H is the thickness of the specimen

Application

• Used to study the interface between two materials, e.g. porcelain fused to metal.

Transverse or Flexural Strength

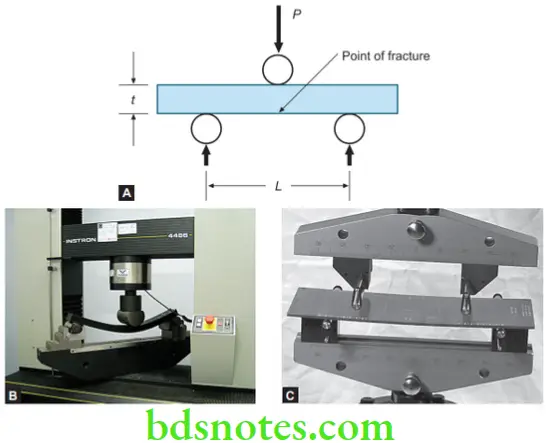
Transverse strength or modulus of rupture, bend strength, or fracture strength is obtained when a load is applied in the middle of a beam supported at each end.

Three types of flexural tests are used

• Three-point flexural test
• Four-point flexural test
• Biaxial flexural test

Three-point flexural test

This test is also called a three-point bending test (3PB).

The flexure strength may be represented by the formula below.

\(\text { Flexural Strength of }=\frac{3 \mathrm{PL}}{2 w t^2}\)

where, P = fracture load in Newtons

L = distance between supports

w = width of the specimens

t = thickness of the specimen

Four-point flexural test

• The addition of a 4th bearing brings a much larger portion of the beam to the maximum stress, as opposed to only the material right under the central bearing. This difference is of prime importance when studying brittle materials, where the number and severity of flaws exposed to the maximum stress is directly related to the flexural strength and crack initiation. The formula for the four-point flexural test is shown below.

\(\text { Flexural Strength } \alpha f=\frac{3 \mathrm{PL}}{4 w t^2}\)

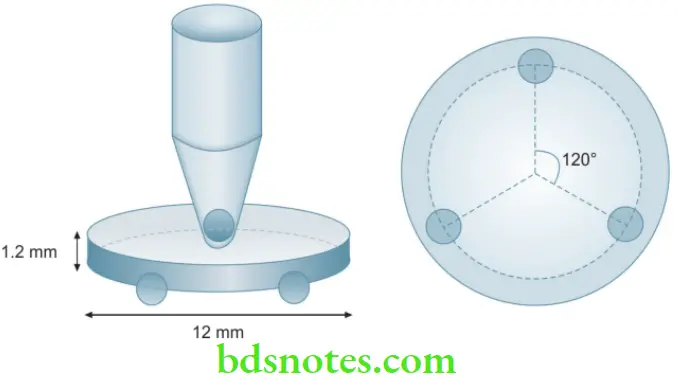
Biaxial flexural test

• This test is used to avoid the problem of edge fractures which can occur with the other flexural tests. Disc-shaped specimens are used of 12 mm diameter and 1.2 mm thickness. The disc is supported by 3 balls (3.2 mm diameter). The load is applied by a round-ended piston.

Application

• Used to test materials like porcelain.

Weibull statistics

Weibull analysis

• Waloddi Weibull invented the Weibull distribution in 1937 and delivered his hallmark paper on this subject in 1951. It is also known as ‘life data analysis’. The primary advantage of Weibull analysis is the ability to provide reasonably accurate failure analysis and failure forecasts.
• Thus it is used to estimate important life characteristics of a product such as reliability or probability of failure at a specific time, the mean life for the product, and the failure rate.
• Although manufacturers provide data on strength values. This typically represents the mean value of a specific test. This may not correlate with its strength and survival probability under clinical situations because in the mouth the restorations experience cyclic loading conditions.
• It would be more useful to know the 95% stress level. This is the stress level below which 95% of the specimens would survive the stress test.
• Dental application Many restorative materials in dentistry are brittle materials like resins and ceramics. These materials do not exhibit a normal or symmetric distribution of strength values. The failure probability of brittle materials like resins and ceramics is best described using Weibull analysis which is based on the concept of the weakest link.

Weibull modulus

The Weibull modulus represents the distribution of flaws in a brittle material or the distribution of strength determined from the fracture probability versus failure test.

Significance

• A low Weibull modulus indicates a material that is inconsistent in strength, has a wide variation of fracture force and, therefore, has low reliability as a restorative material, e.g. Weibull modulus for ceramics ranges from 5-15.
• A higher Weibull modulus indicates a material with greater reliability as a structural material, e.g. Metals that are ductile have a Weibull modulus above 20.

Stress Concentration

A stress concentration (often called stress raiser) is a location in an object where stress is concentrated.

Causes of stress concentration

Knowledge of the causes and effects of stress concentration is important in dental restorations to prevent early failure.

Stress concentrations occur due to

• Structural defects
• Improper design

Structural defects An object is strongest when force is evenly distributed over its area, so a reduction in area, e.g. caused by a crack, results in a localized increase in stress. A material can fail, via a propagating crack, when a concentrated stress exceeds the material’s theoretical cohesive strength.

The real fracture strength of a material is always lower than the theoretical value because most materials contain small cracks or contaminants (especially foreign particles) that concentrate stress.

Design defects A structure should be designed in such a way that stress is evenly distributed. An example of a stress concentration design is a narrow post with supporting a large core. The weakest point of this structure is at the junction of the post and core.

When occlusal forces are applied stress concentration at this point can lead to a fracture. Slight alteration of design can reduce stress concentration. In this case, increasing the diameter of the post and increasing the bulk of the metal at the junction of the post to the core so that the transition is gradual rather than abrupt.

Fatigue

A structure subjected to repeated or cyclic stresses below its proportional limit can produce an abrupt failure of the structure. This type of failure is called fatigue. Fatigue behavior is determined by subjecting a material to cyclic stress of a known value and determining the number of cycles that are required to produce failure. The stresses used in fatigue testing are usually very low. However, the repeated application causes failure.

Application

• Restorations in the mouth are often subjected to cyclic forces of mastication. To last, these restorations should be able to resist fatigue.

Static Fatigue

• It is a phenomenon exhibited by some ceramic materials. These materials support a high static load for a long period and then fail abruptly. This type of failure occurs only when the materials are stored in a wet environment and this property is related to the effect of water on the highly stressed surface of the material.

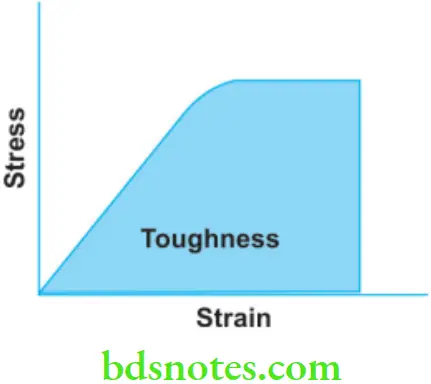
Toughness

• It is defined as the energy required to fracture a material. It is a property of the material which describes how difficult the material would be to break. Toughness is also measured as the total area under the stress-strain curve.

Brittleness

• A brittle material fractures at or near its proportional limit. Brittleness is the opposite of toughness, e.g. glass is brittle at room temperature. It will not bend appreciably without breaking. It should not be wrongly understood that a brittle material lacks strength. From the above example of glass, we see that its shear strength is low, but its tensile strength is very high. If glass is drawn into a fiber, its tensile strength may be as high as 2800 MPa.

Application

• Many dental materials are brittle, e.g. porcelain, cement, dental stone, etc.

Ductility

A material can withstand permanent deformation under a tensile load without rupture. A metal that can be drawn readily into a wire is said to be ductile. Ductility is dependent on tensile strength. Ductility decreases as the temperature is raised.

Ductility may be measured by three methods

• By measuring the percentage elongation after fracture.
• By measuring reduction in the cross-sectional area of fractured ends in comparison to the original area of the wire or rod the method is called reduction in area method.
• By using the cold bend test.

Malleability

• The material can withstand rupture under compression, as in hammering or rolling into a sheet. It is not dependent on strength as is ductility. Malleability increases with the temperature rise.
• The toughness of a material is dependent upon the ductility (or malleability) of the material than upon the flexibility or elastic modulus.

Application of malleability and ductility

• Gold is the most ductile and malleable metal. This property enables manufacturers to beat it into thin foils. Silver is second. Among other metals, platinum ranks third in ductility and copper ranks third in malleability.

Hardness

• Hardness is difficult to define specifically. Numerous factors influence the hardness of a material such as strength, proportional limit, ductility, malleability, etc. In mineralogy, hardness is described as the ability of a material to resist scratching. In metallurgy and most other fields, the resistance to indentation is taken as the measure of hardness. There are many surface hardness tests.

Brinell

• The Brinell hardness scale was developed by a Swedish engineer named Johan August Brinell in 1900. The Brinell test utilizes a 10 mm diameter steel ball as an indenter, applying a uniform 3000 kg (29 kN) force. A smaller amount of force is used on softer materials and a tungsten carbide ball is used for harder materials. The diameter of the indentation left in the test material is measured with a low-powered microscope. The load is divided by the area of the surface of the indentation and the quotient is referred to as the Brinell Hardness Number (BHN).

Application

• Used for measuring the hardness of metals and metallic materials.

Rockwell Hardness Number (RHN)

• Like the BH test, a steel ball or a conical diamond point is used. However, instead of measuring the diameter of the impression, the depth is measured directly by a dial gauge on the instrument.

Application

• The Rockwell test has a wider application for materials since the Brinell test is unsuitable for brittle materials as well as plastic materials.

Vickers Hardness Test (VHN)

• This is also similar to the Brinell test, however, instead of a steel ball, a diamond in the shape of a square pyramid is used. Although the impression is square instead of round. The load is divided by the area of indentation. The length of the diagonals of the indentation (sides of the diamond) are measured and averaged.

Application

• Vickers test is used in the ADA for dental casting golds. This test is suitable for brittle materials and so is used for measuring the hardness of tooth structure.

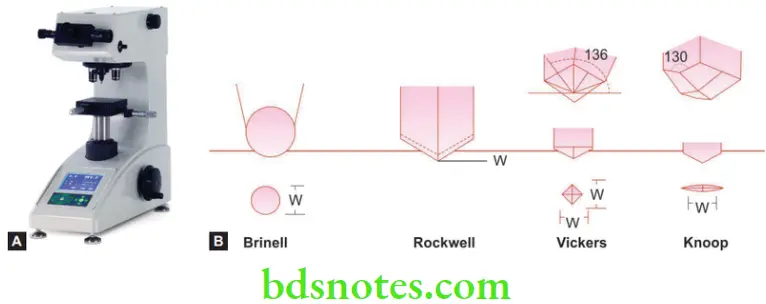
Knoop Hardness Test (KHN)

• A diamond indenting tool is used in a different shape from that of Vickers. The indentation is narrower and elongated. Knoop hardness value is independent of the ductility of the material and values for both exceedingly hard and soft materials can be obtained from this test.
• The Knoop and Vickers tests are classified as microhardness tests. The Brinell and Rockwell tests are classified as macrohardness tests.

The Shore and the Barcol

• These are less sophisticated tests. They are compact portable units (Figs. 2.15A and B). A metal indenter that is spring-loaded is used. The hardness number is based on the depth of penetration and is read directly from a gauge.

Applications

• Used for measuring the hardness of rubber and plastics.

Abrasion Resistance

• Like hardness, abrasion is influenced by some factors. Hardness has often been used to indicate the ability of a material to resist abrasion.

Applications

• It is useful for comparing materials in the same class, e.g. one brand of cement is compared to another and their abrasion resistance is quoted in comparison to one another. However, it may not be useful for comparing materials of different classes like metals and plastics.
• The only reliable test for abrasion is a test procedure that simulates the conditions to which the material will eventually be subjected, e.g. toothbrush abrasion tests.

Rheology

Rheology is the study of the flow of matter. In dentistry, the study of rheology is necessary because many dental materials are liquids at some stage of their use, e.g. molten alloy and freshly mixed impression materials and cements. Other materials appear to be solids but flow over some time.

Terms and Properties in Rheology

Viscosity

• Viscosity is the resistance offered by a liquid when placed in motion, e.g. honey is more viscous than water. It is measured in poise or centipoise (1 cp = 100p).

Rheological Properties

Creep

• Time-dependent plastic deformation or change of shape that occurs when a metal is subjected to a constant load near its melting point is known as creep. This may be static or dynamic in nature.
• Static creep is a time-dependent deformation produced in a completely set solid subjected to constant stress.
• Dynamic creep is produced when the applied stress is fluctuating, such as in a fatigue type test.

Importance

• Dental amalgam has components with melting points that are slightly above room temperature and the creep produced can be very destructive to the restoration, e.g. glass tube fractures under a sudden blow but bends gradually if leaned against a wall.

Flow

• It is somewhat similar to creep. In dentistry, the term flow is used instead of creep to describe the rheology of amorphous substances, e.g. waxes. Although creep or flow may be measured under any type of stress, compression is usually employed for the testing of dental materials.

Thixotropic

• These materials exhibit a different viscosity after it is deformed, e.g. latex paints for ceilings show lower viscosity after they are stirred vigorously. Zinc oxide eugenol cement shows reduced viscosity after vigorous mixing. Dental prophy paste is another example.

Rheological Properties

Relaxation

• Every element in nature attempts to remain in a stable form. If an element is changed from its equilibrium or stable form by either physical or chemical means, it tries to come back to its original form.
• When substances are deformed, internal stresses get trapped because of the displacement of the atoms. The condition is unstable and the atoms try to return to their original positions. This results in a change in shape or contour in the solid as atoms or molecules rearrange themselves. This change in shape due to the release of stresses is known as relaxation. The material is said to warp or distort.
• For example, Waxes and other thermoplastic materials like compounds undergo relaxation after they are manipulated.

Shear Stress And Shear Strain Rate

• A liquid is placed between two plates and the upper plate is moved to the right. The stress required to move the plate is called shear stress (= F/A or force applied/ area of the plate). The change produced is called shear strain rate (= V/d or velocity of plate/distance covered).

Newtonian

• Shear stress and shear strain rate can be plotted. An ideal fluid shows a shear strain rate that is proportional to shear stress. This behavior is called Newtonian.

Pseudoplastic

• If a material’s viscosity decreases with an increase in shear rate, it is said to exhibit pseudoplastic behavior, e.g. elastomeric impression materials when loaded into a tray show a higher viscosity, whereas the same material when extruded under pressure through a syringe tip shows more fluidity.

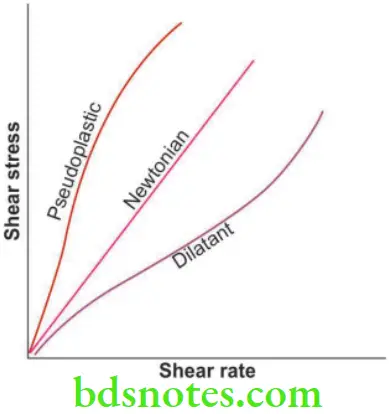
Dilatant

• These are liquids that show higher viscosity as the shear rate increases, e.g. fluid denture base resins.

Physical Properties

Physical properties can be observed or measured without changing the composition of matter. Physical properties are used to observe and describe matter. Physical properties of importance in dentistry include appearance, texture, color, optical properties, odor, glass transition, temperature, melting point, boiling point, density, solubility, polarity, etc.

Forms Of Matter

Change of State

• Matter exists in the forms—of solid, liquid, and gas. The difference in form is mainly due to the difference in energy. Matter is made up of atoms and for these atoms to be held together there must be a force, e.g. when 1 gram of water is to be changed into gaseous state at 100° C, 540 calories of heat are needed (known as heat of vaporization).
• Thus the gaseous state has more energy than the liquid state. Although the molecules in a gas have a certain amount of mutual attraction, they can diffuse readily and need to be confined to keep the gas intact.
• The energy of the liquid is decreased by reducing the temperature sufficiently, a second transformation in state occurs and energy is released in the form of heat (latent heat of fusion). This decrease in energy state changes the liquid to a solid or freezes it.
• The reverse is true when the solid is changed to liquid, i.e., heat is required. The temperature at which it occurs is called fusion temperature.

Melting point

• The melting point (or liquefaction point) of a solid is the temperature at which it changes state from solid to liquid at atmospheric pressure. At the melting point, the solid and liquid phases exist in equilibrium.

Rheological Properties

Boiling point

• The boiling point of a substance is the temperature at which the vapor pressure of the liquid equals the pressure surrounding the liquid and the liquid changes into a vapor. The boiling point of a liquid varies depending on the surrounding environmental pressure.

Density

• The density, or more precisely, the volumetric mass density, of a substance is its mass per unit volume. The symbol most often used for density is ρ (the lowercase Greek letter rho). Mathematically, density is defined as mass divided by volume–

\(\rho=\frac{m}{v}\)

where ρ is the density, m is the mass, and V is the volume.

• In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate—this quantity is more specifically called specific weight.
• For a pure substance, the density has the same numerical value as its mass concentration. Different materials usually have different densities. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure.
• To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity “relative density” or “specific gravity”, i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one means that the substance floats in water.
• The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume.

Glass Transition Temperature (Tg)

• The glass transition temperature (Tg) is the temperature at which an amorphous solid becomes soft upon heating or brittle upon cooling. The Tg is one of the most important properties of any epoxy and is the temperature region where the polymer transitions from a hard, glassy material to a soft, rubbery material. The glass transition temperature is always lower than the melting temperature (Tm) of the crystalline state of the material if one exists.
• The glass transition temperature is the most important property of a polymer. The value of the glass transition temperature is directly related to the mechanical properties (strength, hardness, brittleness, elongation, etc.).
• The glass transition temperature is more important in plastics applications than the melting point, because it tells a lot about how the polymer behaves under ambient conditions. If a polymer’s glass transition temperature is well above ambient room temperature, the material behaves like a brittle glassy polymer (it is stiff with low impact resistance). Conversely, if the
• Tg is well below room temperature, the material is what is commonly termed a rubber or elastomer (soft and easily stretched). Those materials whose Tg is reasonably close to the ambient temperature exhibit plastic material behavior (strong and tough with good impact resistance). There are chemical compounds known as plasticizers that are used to decrease the glass transition temperature.

Solubility

• Solubility is the property of a solid, liquid, or gaseous chemical substance called solute to dissolve in a solid, liquid, or gaseous solvent to form a homogeneous solution of the solute in the solvent.
• Restorations placed in the oral cavity are required to be insoluble in oral fluids. The tendency of cement to dissolve in the oral fluids can lead to marginal ditching, microleakage, recurrent caries, and ultimately failure of the restoration.

Thermal properties

Thermal properties are the response of a material to the application of heat.

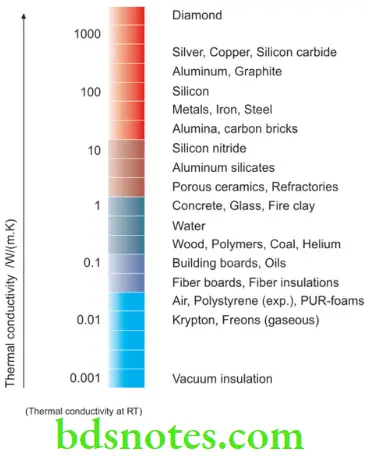
Thermal conductivity

• Thermal conductivity is defined as the property of a material that indicates its ability to conduct heat through its body under a steady state condition. It is measured in watts per meter per degree Kelvin (W/(mK)). In Imperial units, thermal conductivity is measured in BTU/(hr.ft.°F)
• It is defined as the quantity of heat in calories per second passing through a material 1 cm thick with a cross-section of 1 cm2 having a temperature difference of 1 K (1°C) and is measured under a steady-state condition in which the temperature gradient does not change.
• Thermal conductivity depends on many properties of a material, its structure, and temperature. The transfer of heat within a material takes place by conduction; in this process, the materials do not move as a whole but the energy flows through the body of the material by the transfer of the molecular kinetic energy. Various materials exhibit varying degrees of thermal conductivity.

• The divided bar method (steady-state method) is the most common way of measuring thermal conductivity. The sample to be measured is placed between two samples of known conductivity (usually brass plates). The sample is placed at the top of the vertical setup and the known conductivity brass bars are kept at the bottom. To stop any convection within the sample, heat is supplied at the top and moved downwards. After approximately 10 minutes, the measurements are taken after the whole sample becomes equally hot.

Thermal diffusivity

Thermal diffusivity measures the ability of a material to conduct thermal energy relative to its ability to store thermal energy. Thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has an SI unit of m²/s. Thermal diffusivity is usually denoted by α but a, κ, K, and D are also used. The formula is

\(\alpha=\frac{\mathrm{k}}{\rho \times C_\rho}\)

κ is thermal conductivity (W/(mK))

ρ is density (kg/m³)

Cρ is specific heat capacity (J/(kg K))

Thermal Expansion

• Thermal energy is due to the kinetic energy (internal energy) of the atoms or molecules at a given temperature. At temperatures above absolute zero, atoms are in a constant state of vibration. The average amplitude of vibration depends upon the temperature.
• The higher the temperature, the greater will be the kinetic energy and the amplitude of the atomic (or molecular) vibration increases. As the amplitude and internal energy of the atoms increase, the interatomic spacing increases as well. The gross effect is an expansion known as thermal expansion.
• If the temperature continues to increase, the interatomic spacing will increase and eventually a change of state will occur (e.g. solid to liquid).

Coefficient of Thermal Expansion (CTE)

• When a substance is heated, the kinetic energy of its molecules increases. This usually results in an expansion called thermal expansion.
• The coefficient of thermal expansion describes how the size of an object changes with a temperature change. Specifically, it measures the fractional change in size per degree change in temperature at a constant pressure.

Measurement of CTE

Several types of coefficients have been developed—volumetric, area, and linear. Which is used depends on the particular application. For solids, one might only be concerned with the change along a length, or area. The volumetric thermal expansion coefficient is commonly used for fluids and gases. It is normally quoted in parts per million per degree Celsius rise in temperature (ppm/K).

\(\alpha=\frac{\Delta \mathrm{L}}{\mathrm{L} \times \Delta \mathrm{T}}\)

α (alpha) is CTE

L is the original length of the material

ΔL (delta L) is change in length

ΔT (delta T) is the change in temperature

Negative thermal expansion

• Several materials contract on heating within certain temperature ranges; this is usually called negative thermal expansion. For example, the coefficient of thermal expansion of water drops to zero as it is cooled to 3.983°C and then becomes negative below this temperature; this means that water has a maximum density at this temperature, and this leads to bodies of water maintaining this temperature at their lower depths during extended periods of sub-zero weather. Another example is pure silicon. It has a negative coefficient of thermal expansion for temperatures between about 18 and 120 Kelvin.

Significance of CTE

• The mismatch of thermal expansion and contraction between restorative materials and the tooth may cause stresses at their interface, which may lead to microleakage.
• Metal ceramics restorations require a close match between the CTE of the alloy and porcelain to reduce stresses in the porcelain. These stresses can cause immediate or delayed cracking in the ceramic.
• An inlay wax pattern created in the mouth may contract when transferred to the colder room.
• Denture teeth set in wax may shift slightly when room temperature changes.

Optical properties and color

Light is a form of electromagnetic radiant energy within a certain portion of the electromagnetic spectrum that can be detected by the human eye. The eye is sensitive to wavelengths from approximately 400 nm (violet) to 700 nm (dark red). The combined intensities of the wavelengths present in a beam of light determine the property called color.

For an object to be visible, either it must emit light or it must reflect or transmit light falling upon it from an external source. Objects of dental interest generally transmit light. The incident light is usually polychromatic (mixed light of various wavelengths).

The reaction of an object to the incident light is to selectively absorb and/or scatter certain wavelengths. The spectral distribution of the transmitted or reflected light will resemble that of the incident light although certain wavelengths will be reduced in magnitude.

Cone-shaped cells in the retina are responsible for color vision in humans. The eye is most sensitive to light in the green-yellow region and least sensitive at either extreme (i.e., red or blue).

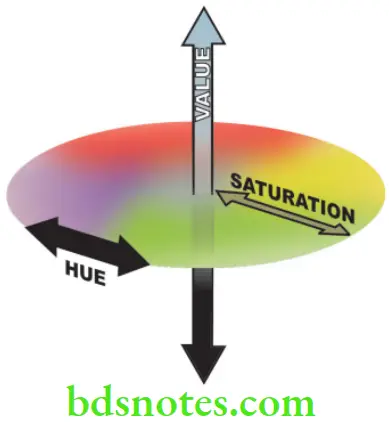
Dimensions of Color

The three dimensions of color are — hue, value, and chroma.

Hue

Refers to the basic color of an object, e.g. whether it is red, green, or blue.

Value

Colors can be separated into ‘light’ and ‘dark’ shades. The value represents the amount of lightness or darkness in the color. This lightness which can be measured independently of the hue is called value.

Chroma

A particular color may be dull or more ‘vivid’, this difference in color intensity or strength is called chroma. Chroma represents the degree of saturation of a particular hue (color). In other words, the higher the chroma, the more intense is the color. Chroma cannot exist by itself and is always associated with hue and value. The three dimensions of color are represented.

Measurement of Color

• One of the most commonly used methods to define and measure color quantitatively is the Munsell System. It is a coordinate system which can be viewed as a cylinder. The lines are arranged sequentially around the perimeter of the cylinder, while the chroma increases along a radius from the axis. The value coordinate varies along the length of the cylinder from black at the bottom to neutral grey at the center to white at the top.

Metamerism

• The appearance of an object depends on the type of light by which the object is viewed. Daylight, incandescent lamps, and fluorescent lamps are all common sources of light in the dental operatory. Objects that appear to be color-matched under one type of light may appear very different under another light source. This phenomenon is called metamerism.

Tooth Esthetics

Reproducing a tooth—both art and science. The esthetics of a dental restoration is determined by

• Shape
• Color
• Texture

The shade and color of a tooth is a complex interplay of many factors. The color of the tooth is determined by the shade, thickness, and composition of the enamel and dentin, the pulp chamber, extrinsic stains, color reflections from the gum and adjacent teeth, and the incident light itself.

Light is a form of energy and must obey the basic law of conservation of energy which states that energy cannot be created or destroyed but only changed from one form into another or transferred from one object to another.

Transparency, Translucence, and opacity

• A transparent object allows all the light to pass through the object, whereas a translucent object allows only partial passage of light. For example, plain glass is transparent, whereas frosted glass is translucent. An object which does not allow any passage of light is said to be opaque.

Relevance

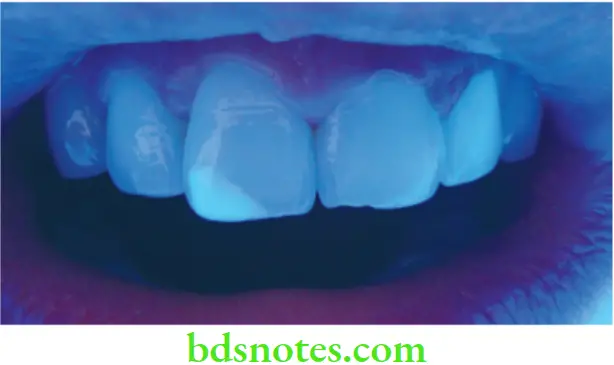
• Teeth and oral tissue are translucent and allow passage of some of the incident light. In some individuals, the enamel may be translucent or in rare circumstances transparent. This may be particularly evident in the incisal edges of upper or lower incisors. Metal-ceramic restorations are opaque unlike natural teeth which are translucent (Fig. 2.21). One of the reasons for improved esthetics with all-ceramic restorations is improved translucency.

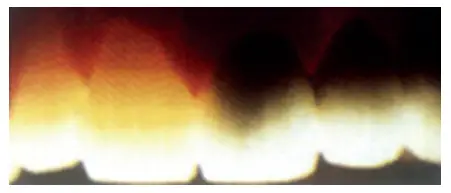
Fluorescence

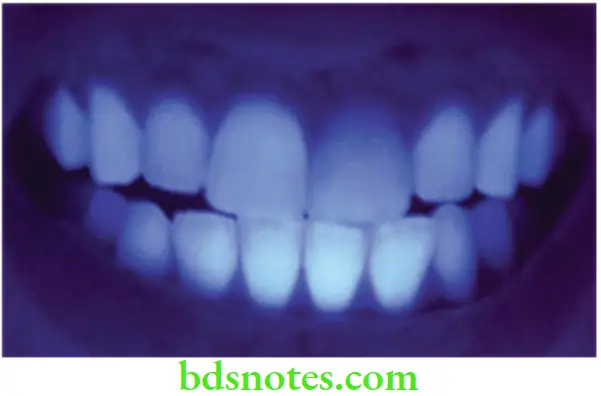
• Natural tooth structure also absorbs light of wavelengths that are too short to be visible to the human eye. These wavelengths between 300 to 400 nm are referred to as near ultraviolet. Natural sunlight, photoflash lamps, certain types of vapor lamps, and the ultraviolet lights used in decorative lighting are all sources containing substantial amounts of near U-V radiation and invisible U-V light (also called black light).
• This energy that the tooth absorbs is converted into light with larger wavelengths, in which case the tooth becomes a light source. The phenomenon is called fluorescence. The emitted light is primarily in the 400-450 nm range, having a blue-white color. Improved fluorescence adds esthetic value to artificial restorations.

Relevance

• In UV light a natural tooth emits a weak whitish-blue fluorescence. This should be taken into account when selecting restoratives. If restorative materials do not offer this property of fluorescence, they will look dark in UV light, and the restored tooth will stand out against the other teeth in the mouth. Some patients want their restorations to match natural teeth under fluorescent light conditions, e.g. in stage shows and discotheques. Some porcelain restorations can match the natural teeth under fluorescent lighting.

Clinical Considerations

• Esthetics play a very important role in modern dental treatment. The ideal restorative material should match the color of the tooth it restores. In maxillofacial prosthetics, the color of the gums, external skin, and the eyes have to be duplicated.
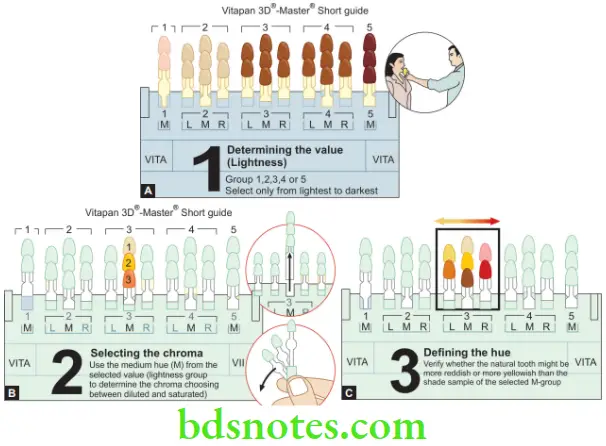
• Clinically in the operatory or dental lab, color selection is usually done by the use of shade guides. These are used in much the same way as paint chips are used to select the color for house paint. The process of selection is described in.

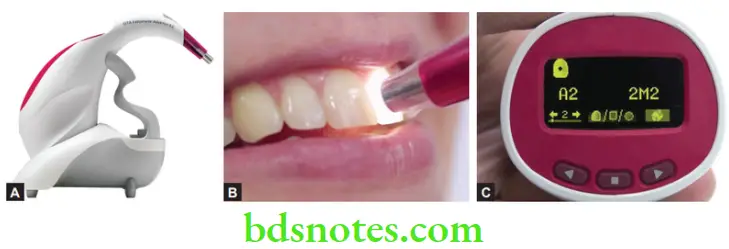
• Digital shade guides are also available. The probe is simply placed against the tooth and on the press of a button, the reading is displayed on the screen. The device is also useful to measure the progress of bleaching.

Radiological properties

Radiopacity and Radiolucency

• Radiopacity may be defined as the quality or property of a material to obstructs the passage of radiant energy, such as X-rays. Thus materials that inhibit the passage of electromagnetic radiation are called radiopaque. On the other hand, those that allow radiation to pass more freely are referred to as radiolucent.

Significance in dentistry

• Radiography plays a significant role in dentistry. It is very useful as a diagnostic tool. Radiographs help to detect problems within the restorations, teeth, bones, etc. Manufacturers add certain elements to many dental materials in order to make them radiopaque.
• Commonly used elements are heavy metal glasses (strontium or barium glasses) compounds (barium sulfate) and metal oxides (zirconium dioxide and ytterbium oxide. Pure polymers like acrylic resins and bis-GMA are radiolucent. Composites, ceramics, and metals are radiopaque, with metals showing the highest radiopacity.

Measurement of radiopacity

• Human tissues like teeth, bone, and soft tissue have varying levels of radiopacity. Within the tooth, the enamel is more radiopaque than dentin. Radiopacity similar to hard tissues of the body provides an optimal contrast for diagnosis. If the radiopacity of the material is too low, it will not be visible. Generally, a restorative material should have radiopacity slightly greater than that of enamel to present a contrast. The thickness of the material also affects its radiographic properties. Radiopacity increases with an increase in thickness.
• Aluminum is used as a standard to measure radiopacity. The radiopacity of a material is expressed as the equivalent thickness of aluminum (millimeters of aluminum). Typically an aluminum step wedge is used for comparative studies. Specimens of specified thickness are radiographed together with the step wedge for comparison.

Magnetic properties of matter

• Magnetism is a class of physical phenomena that are mediated by magnetic fields. Electric currents and the fundamental magnetic moments of elementary particles give rise to a magnetic field. All matter exhibits magnetic properties when placed in an external magnetic field.
• Aristotle attributed the first of what could be called a scientific discussion on magnetism to Thales of Miletus, who lived from about 625 BCE to about 545 BCE. Around the same time, in ancient India, the Indian surgeon, Sushruta, was the first to make use of the magnet for surgical purposes. The Chinese were believed to be using the compass for navigation prior to the Europeans. Alexander Neckam, by 1187, was the first in Europe to describe the compass and its use for navigation.

Classification

Depending on whether there is an attraction or repulsion by the pole of a magnet, matter is classified as being either

• Paramagnetic—attracted to a magnetic field
• Diamagnetic—repulsed by a magnetic field

Terms

• Magnetic field A magnetic field is the magnetic effect of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude (or strength).

• Magnetic moment The magnetic moment (or magnetic dipole moment) of an object is a measure of the object’s tendency to align with a magnetic field. It is a vector quantity. The object will tend to align itself so that its magnetic moment vector is parallel to the magnetic field lines. Some materials like iron (ferromagnets) have permanent magnetic moments. Most materials do not have permanent moments.
• Ferromagnetism It is the basic mechanism by which certain materials can retain their magnetization when the external field is removed. Examples of ferromagnetic substances include iron, nickel, cobalt, and some of the rare earth elements, such as gadolinium and dysprosium.
• Nonmagnetic substances Substances that are negligibly affected by magnetic fields are known as nonmagnetic substances. They include copper, aluminum, gases, and plastic. Pure oxygen exhibits magnetic properties when cooled to a liquid state.
• Magnetocrystalline anisotropy Magnets are capable of producing high forces relative to their size due to the property of magnetocrystalline anisotropy. Samarium-cobalt (SmCo5) and neodymium-iron-boron magnets (Nd2Fe14B) magnets not only have the property of magnetocrystalline anisotropy, but they also have high coercivity.
• Coercivity It is the ability of the magnet to resist demagnetization. Materials with high magnetic anisotropy usually have high coercivity.

Types

• Ceramic magnets are used in refrigerators and elementary-school science experiments and contain iron oxide in a ceramic composite. Most ceramic magnets, sometimes known as ferric magnets, aren’t particularly strong.
• Alnico magnets are made from aluminum, nickel, and cobalt. They’re stronger than ceramic magnets, but not as strong as the ones that incorporate a class of elements known as rare-earth metals.
• Neodymium magnets contain iron, boron, and the rare-earth element neodymium. Compared to other available magnets, neodymium magnets are the strongest permanent magnets available. Today they are used in computer hard drives, speakers, electric motors, wind turbines, etc.
• Samarium cobalt magnets combine cobalt with the rare-earth element samarium.
• Others In the past few years, scientists have also discovered magnetic polymers or plastic magnets. Some of these are flexible and mouldable. However, some work only at extremely low temperatures, and others pick up only very lightweight materials, like iron filings.

Uses

Magnetic resonance imaging

• Magnetic resonance imaging (MRI), nuclear magnetic resonance imaging (NMRI), or magnetic resonance tomography (MRT) is a medical imaging technique used in radiology to investigate the anatomy and physiology of the body in both health and disease. MRI scanners use strong magnetic fields and radiowaves to form images of the body. The technique is widely used in hospitals for medical diagnosis.

In dentistry

• Magnets have generated great interest within dentistry. They have been used for various applications in orthodontics and prosthodontics. Earlier use of magnets was limited due to the unavailability of small-size magnets, but after the introduction of rare earth magnets and their availability in smaller sizes, their use has increased considerably. They can be placed within prostheses without being obtrusive.

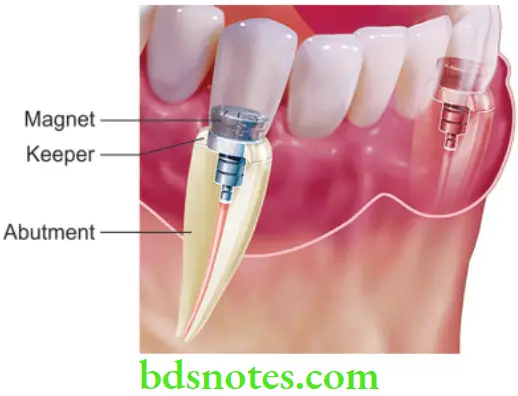
In orthodontics, Their main use in orthodontics has been for tooth movement

In prosthodontics, They are primarily used as retentive aids in maxillofacial prosthesis and in tooth and implant support.